Kimi论文——Muon优化器原理/torch优化器

众所周知，目前主流应用的优化器是AdamW，不过一个新的优化器 Muon（仅仅发布在Github上）似乎比 AdamW优化器能够实现更加优异的效果，于此同时Kimi也出了一篇新的论文就是使用 Muon优化器，有必要了解一些这个优化器以及测试一下这个优化器效果。

AdamW优化器

Adam优化器在这篇blog有介绍，主要回顾一下AdamW，AdamW是 Adam 优化器的一个变种，旨在改进 L2 正则化的处理。AdamW 的数学公式可以通过以下几个步骤来描述：

1. 动量估计

AdamW 基于梯度的一阶矩（平均梯度）和二阶矩（梯度的平方）进行估计。对于每个参数 $θ_{t}$ ，算法计算以下量：

一阶矩（梯度的加权平均）：
$m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t}$

其中 $g_{t}$ 是当前时刻的梯度， $β_{1}$ 是衰减率，通常设置为 0.9。

二阶矩（梯度平方的加权平均）：
$v_{t} = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2}$

其中 $β_{2}$ 是衰减率，通常设置为 0.999。

2. 偏置校正

由于在训练初期，动量估计 $m_{t}$ 和 $v_{t}$ 都会偏向零，因此需要进行偏置校正。偏置校正公式如下：

偏置校正后的动量估计：
${\hat{m}}_{t} = \frac{m_{t}}{1 - β_{1}^{t}}$
偏置校正后的二阶矩估计：
${\hat{v}}_{t} = \frac{v_{t}}{1 - β_{2}^{t}}$

3. 更新规则

AdamW 的更新规则与传统的 Adam 更新规则相似，但加入了权重衰减（L2 正则化），权重衰减是通过 $λ$ 控制的，其中 $λ$ 是 L2 正则化项的超参数。

更新公式为（Adam计算公式中只有前面两个部分）：

θ_{t} = θ_{t - 1} - \frac{η}{\sqrt{{\hat{v}}_{t}} + ϵ} \cdot {\hat{m}}_{t} - η λ θ_{t - 1}

其中：

$θ_{t - 1}$ 是上一时刻的参数值， $θ_{t}$ 是当前时刻的参数值。
$η$ 是学习率。
$ϵ$ 是一个小常数，用于避免除零错误，通常设置为 $10^{- 8}$ 。
$λ$ 是权重衰减的超参数（AdamW 中引入的主要不同点）。
${\hat{m}}_{t}$ 和 ${\hat{v}}_{t}$ 是经过偏置校正的一阶和二阶矩。

Muon优化器

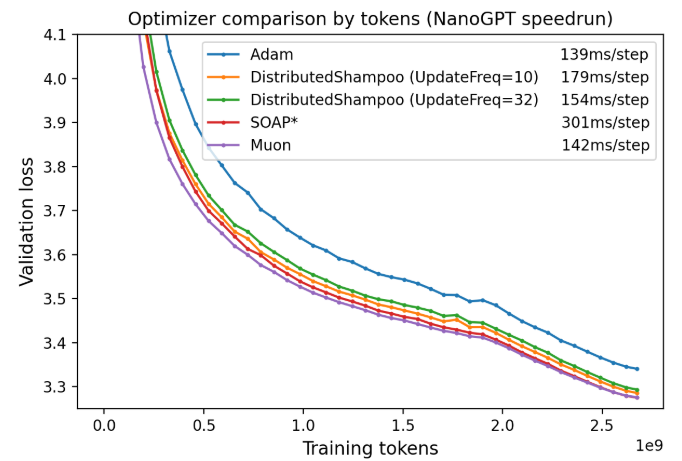
官方提供的Muon效果，Muon（MomentUm Orthogonalized by Newton-Schulz）通过获取由 SGD-momentum 生成的更新，然后对每个更新应用Newton-Schulz (NS)迭代作为后处理步骤，再将其应用于参数，从而优化二维神经网络参数。其更新范式为：

\begin{aligned} Compute gradient G_{t} \leftarrow \nabla_{θ} L_{t} (θ_{t - 1}) \\ B_{t} \leftarrow μ B_{t - 1} + G_{t} \\ O_{t} \leftarrow NewtonSchulz 5 (B_{t}) \\ Update parameters θ_{t} \leftarrow θ_{t - 1} - η O_{t} \end{aligned}

其中 $η$ 为学习率。简单回顾更新方式，容易发现 Muon是一种类似Adam的的自适应学习率的优化器。值得注意的是， Muon对参数形状有要求，根据作者给出的要求：1、不能直接对embedding layer以及最后的全连接层使用，这部分要用其他优化器；2、为了将其与 4D 卷积滤波器一起使用，最好将它们的最后三个维度展平。
在blog中介绍一点，从实验中发现对于Transformer类型的模型，对于一些参数通常是低秩的矩阵，所有神经元的更新都由少数几个方向主导。作者推测，正交化能有效增加其他 “稀有方向 ”的规模，这些方向在更新中的影响很小，但对学习却很重要。
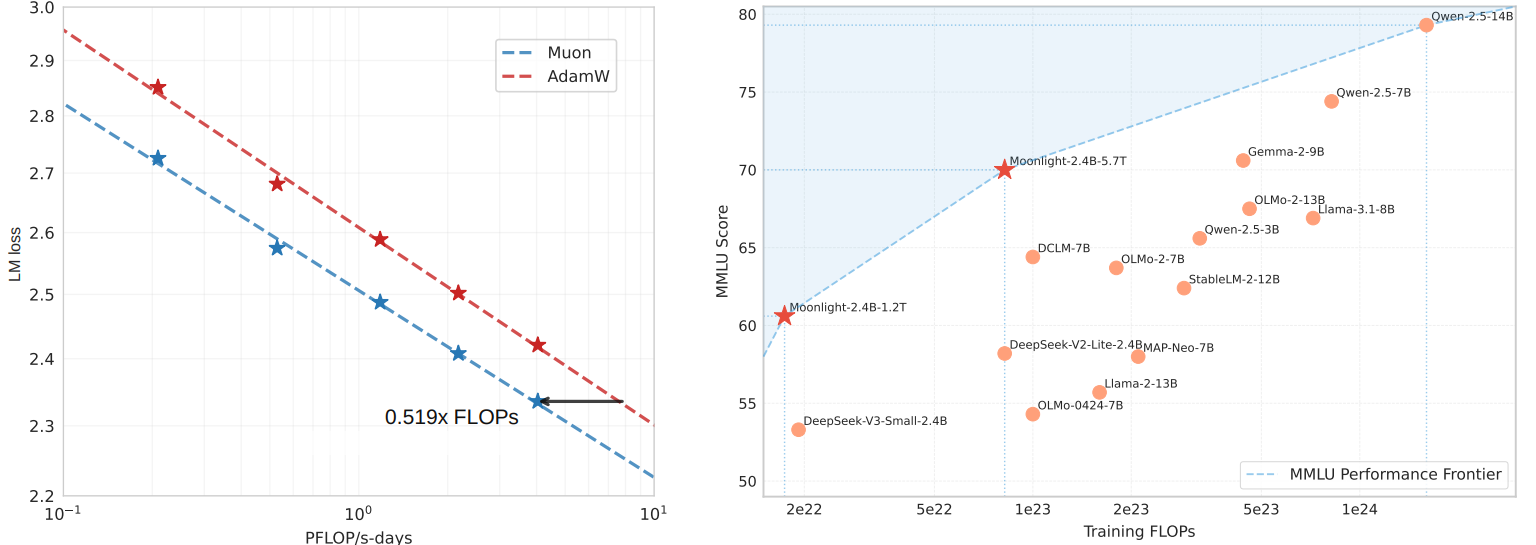
回顾Kimi论文中提到的，基于 Muon优化器提出 Moonlight所展现的实验效果如下：

在kimi论文中对于Muon优化器改进如下：
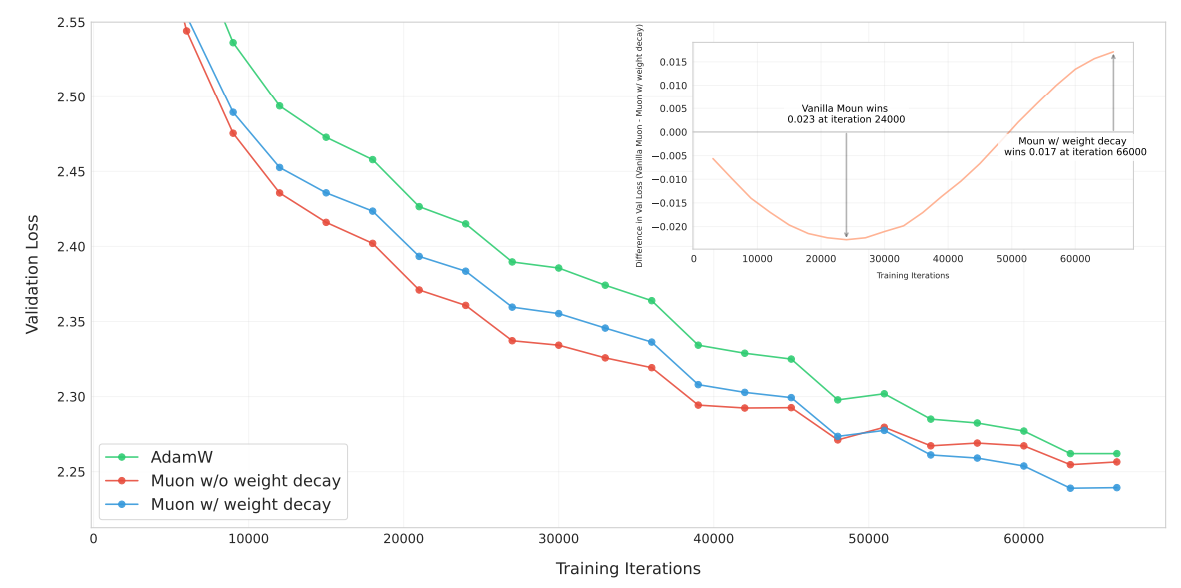
1、增加了Weight Decay：这点主要是希望match AdamW里的Weight Decay，如果不加入WD的话，收敛速度的优势会随着训练Token慢慢消失。这是考虑到在低精度训练的时候，如果不控制权重的大小，会有表示精度的问题——浮点数的二进制表示方式决定了，在数值较大的范围内，浮点数表示的固定间隔会很大:

θ_{t} \leftarrow θ_{t - 1} - η (O_{t} + λ θ_{t - 1})

2、通过学习率调节增加了RMS控制：由于Muon的每次更新的RMS理论值在 $\sqrt{1 / max ({fan}_{in}, {fan}_{out})}$ ，因此相应地在O上乘以 $0.2 * \sqrt{m a x ({fan}_{in}, {fan}_{out})}$ ，把更新步的RMS保持与Adam一致。

θ_{t} \leftarrow θ_{t - 1} - η (O_{t} * 0.2 * \sqrt{m a x (fan_in, fan_out)} + λ θ_{t - 1})

总结

总的来说，Muon优化器区别于 AdamW而言：因为只存储动量（ AdamW需要存储1，2阶动量）对于显存的占用是明显减少了，代价是稍多的通讯量，以及Newton-Schulz迭代步带来的额外计算延迟

代码使用

Muon给出了示例，不过需要注意的是“ ≥2D parameters in the body of the network – these should be optimized by Muon”也就是使用之前需要对模型的参数进行划分。实际测试结果如下：
GPU 2080 Ti-22G 数量： 1 显存： 11 GB
CPU AMD EPYC 7302 16-Core Processor 实例内存： 30G
最高CUDA版本 12.2
显卡驱动版本 535.216.03

Some warnings:- This optimizer should not be used for the embedding layer, the final fully connected layer,or any {0,1}-D parameters; those should all be optimized by a standard method (e.g., AdamW).

To use it with 4D convolutional filters, it works well to just flatten their last 3 dimensions.

torch优化器内部结构

在pytoch常用的优化器中(比如:torch.optim.SGD等)优化算法均继承于Optimizer，所有优化器的基类Optimizer。定义如下:

class Optimizer(object):
    def __init__(self, params, defaults):        
        self.defaults = defaults # 优化器的超参数
        self.state = defaultdict(dict) # 参数缓存
        self.param_groups = [] # 管理的参数组，是一个list，其中每个元素是一个字典，顺序是params，lr，momentum，dampening，weight_decay，nesterov

defaults：存储的是优化器的超参数，例子如下：

{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}

state：参数的缓存，例子如下

defaultdict(<class 'dict'>, {tensor([[ 0.3864, -0.0131],
        [-0.1911, -0.4511]], requires_grad=True): {'momentum_buffer': tensor([[0.0052, 0.0052],
        [0.0052, 0.0052]])}})

param_groups：管理的参数组，是一个list，其中每个元素是一个字典，顺序是params，lr，momentum，dampening，weight_decay，nesterov，例子如下：

[{'params': [tensor([[-0.1022, -1.6890],[-1.5116, -1.7846]], requires_grad=True)], 'lr': 1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]

在Optimizer中还有如下方法
zero_grad()：清空所管理参数的梯度，PyTorch的特性是张量的梯度不自动清零，因此每次反向传播后都需要清空梯度。
step()：执行一步梯度更新，参数更新
add_param_group()：添加参数组
load_state_dict() ：加载状态参数字典，可以用来进行模型的断点续训练，继续上次的参数进行训练
state_dict()：获取优化器当前状态信息字典

在Muon优化器内部设计(不去考虑分布式训练过程)

class Muon(torch.optim.Optimizer):
    """
    Muon - MomentUm Orthogonalized by Newton-schulz
    """
    def __init__(self, params, lr=0.02, weight_decay=0.01, momentum=0.95, nesterov=True, ns_steps=5, rank=0, world_size=1):
        self.rank = rank
        self.world_size = world_size
        defaults = dict(lr=lr, weight_decay=weight_decay, momentum=momentum, nesterov=nesterov, ns_steps=ns_steps)
        params: list[Tensor] = [*params]
        param_groups = []
        for size in {p.numel() for p in params}:
            b = torch.empty(world_size, size, dtype=torch.bfloat16, device="cuda")
            group = dict(params=[p for p in params if p.numel() == size],
                         update_buffer=b, update_buffer_views=[b[i] for i in range(world_size)])
            param_groups.append(group)
        super().__init__(param_groups, defaults)
    @torch.no_grad()

参考

1、https://arxiv.org/pdf/2502.16982
2、https://spaces.ac.cn/archives/10739
3、https://spaces.ac.cn/archives/10592
4、https://kellerjordan.github.io/posts/muon/
5、https://github.com/KellerJordan/Muon
6、https://www.zhihu.com/question/13193527053/answer/109342120565
7、https://datawhalechina.github.io/thorough-pytorch/%E7%AC%AC%E4%B8%89%E7%AB%A0/3.9%20%E4%BC%98%E5%8C%96%E5%99%A8.html