深度学习混合专家模型（MoE）/KV-cache原理及其代码

主要介绍 混合专家模型（MoE）、KV cache并且结合代码进行解释

1、混合专家模型（MoE）

参考HuggingFace中介绍：混合专家模型主要由两部分构成：
1、稀疏的MoE层：这些层代替了传统 Transformer 模型中的前馈网络 (FFN) 层。MoE 层包含若干“专家”(例如 8 个)，每个专家本身是一个独立的神经网络。在实际应用中，这些专家通常是前馈网络 (FFN)，但它们也可以是更复杂的网络结构，甚至可以是 MoE 层本身，从而形成层级式的 MoE 结构。
2、门控网络/路由（Gate Layer/route Layer）：这个部分用于决定哪些令牌 (token) 被发送到哪个专家。例如，在下图中，“More”这个令牌可能被发送到第二个专家，而“Parameters”这个令牌被发送到第一个专家。有时，一个令牌甚至可以被发送到多个专家。令牌的路由方式是 MoE 使用中的一个关键点，因为路由器由学习的参数组成，并且与网络的其他部分一同进行预训练。

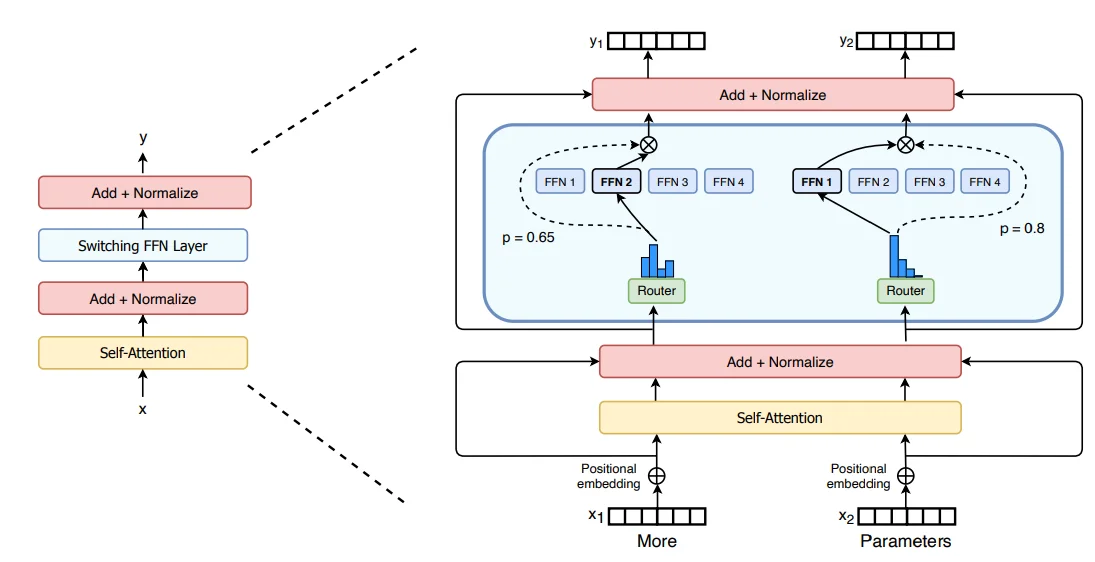
换言之也就是说：将原始的Transformer框架中的FFN Layer（全连接层）替换成一个由Gate Layer和若干的FFN Layer组成的结构，通过Gate来确定一个输入将会被那些FFN进行处理，而后对被FFN处理后的内容进行加权处理。

---

1、稠密MoE和 稀疏MoE

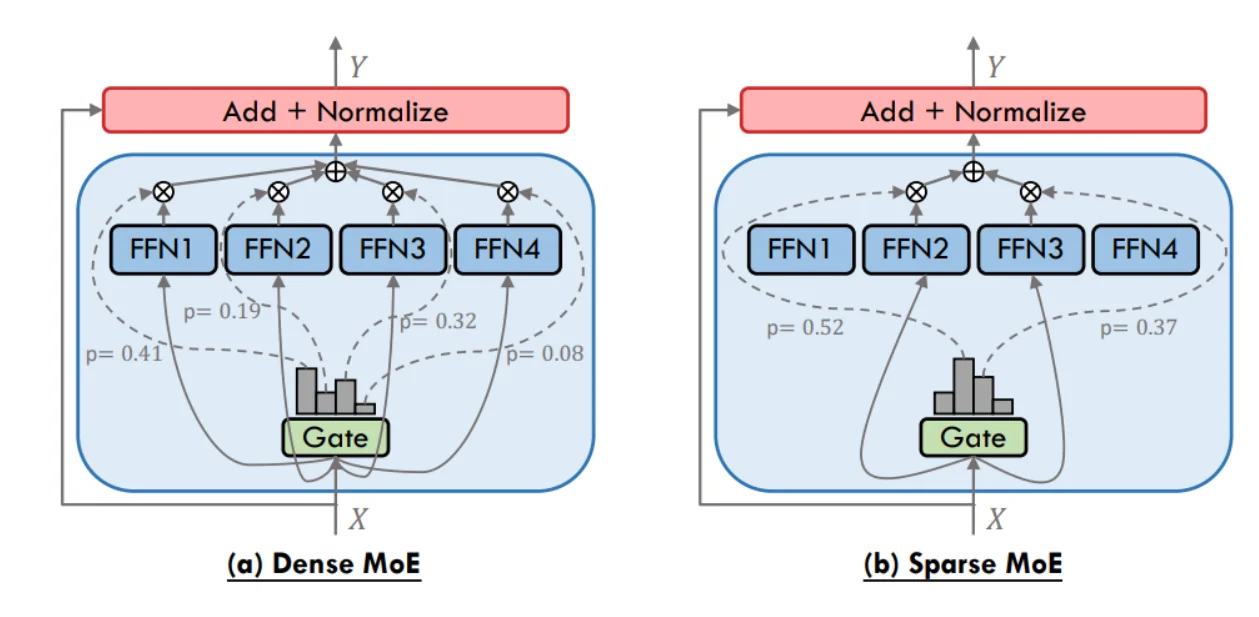
检验而言：如上图所示，对于稠密的MoE（Dense MoE）而言（假设4个FFN）在通过Gate处理之后输入X要通过每一个FFN进行处理，而对于稀疏的MoE（Sparse MoE）而言，通过Gate处理只去选择部分FFN进行处理

2、MoE原理

1、Gate/route原理
输入数据$x$，通过一个线性层进行处理：

\[s = W_{gate}x+b\]

对于得到的score再通过Softmax函数处理，得到一个概率分布：

\[g(x)=\text{Softmax}(s)\]

对于稀疏的MoE而言还需要去选择部分专家进行激活：

\[h(x)=\frac{g(x)_{i\in Top-k}}{\sum_{i\in Top-k }g(x)_i}\]

原理很简单，结合代码分析（以Deepseek-v3代码为例）

class Gate(nn.Module):
    """
    Gating mechanism for routing inputs in a mixture-of-experts (MoE) model.
    """
    def __init__(self, args: ModelArgs):
        """
        Initializes the Gate module.

        Args:
            args (ModelArgs): Model arguments containing gating parameters.
        """
        super().__init__()
        self.dim = args.dim
        self.topk = args.n_activated_experts # 选择多少个专家进行使用
        self.n_groups = args.n_expert_groups # Gate数量
        self.topk_groups = args.n_limited_groups # 对于gate中分组数
        self.score_func = args.score_func
        self.route_scale = args.route_scale
        self.weight = nn.Parameter(torch.empty(args.n_routed_experts, args.dim))
        self.bias = nn.Parameter(torch.empty(args.n_routed_experts)) if self.dim == 7168 else None

    def forward(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """
        Forward pass for the gating mechanism.

        Args:
            x (torch.Tensor): Input tensor.

        Returns:
            Tuple[torch.Tensor, torch.Tensor]: Routing weights and selected expert indices.
        """
        scores = linear(x, self.weight) # 计算wx+b
        # 归一化处理
        if self.score_func == "softmax":
            scores = scores.softmax(dim=-1, dtype=torch.float32)
        else:
            scores = scores.sigmoid()
        original_scores = scores

        if self.bias is not None:
            scores = scores + self.bias
        if self.n_groups > 1:
            # 如果Gate数量>1
            scores = scores.view(x.size(0), self.n_groups, -1)
            if self.bias is None:
                group_scores = scores.amax(dim=-1)
            else:
                group_scores = scores.topk(2, dim=-1)[0].sum(dim=-1)
            indices = group_scores.topk(self.topk_groups, dim=-1)[1]
            mask = torch.zeros_like(scores[..., 0]).scatter_(1, indices, True)
            scores = (scores * mask.unsqueeze(-1)).flatten(1)
        indices = torch.topk(scores, self.topk, dim=-1)[1]
        weights = original_scores.gather(1, indices)
        if self.score_func == "sigmoid":
            weights /= weights.sum(dim=-1, keepdim=True)
        weights *= self.route_scale
        return weights.type_as(x), indices

整个过程分析：输入数据x（假设维度为：（bs, num_tokens, embed_dim）），通过线性（W：（n_routed_experts，embed_dim）计算得到：bs，num_tokens，n_routed_experts）和归一化处理：（bs，num_tokens， n_routed_experts）这样一来就可以知道每个tokens的一个分布概率（到底要走哪一个FFN）。如果n_expert_groups数量>1，也就是说如果Gate数量不止一个，那么也就只需要去选择topK即可然后用一个mask将其他的给mask掉即可（scores = (scores * mask.unsqueeze(-1)).flatten(1)）然后再去对挑选得到的Gate选择topk（indices = torch.topk(scores, self.topk, dim=-1)[1]）

2、FFN Layer原理

这部分代码就比较简单（直接用线性层处理即可）：

class Expert(nn.Module):
    """
    Expert layer for Mixture-of-Experts (MoE) models.

    Attributes:
        w1 (nn.Module): Linear layer for input-to-hidden transformation.
        w2 (nn.Module): Linear layer for hidden-to-output transformation.
        w3 (nn.Module): Additional linear layer for feature transformation.
    """
    def __init__(self, dim: int, inter_dim: int):
        """
        Initializes the Expert layer.

        Args:
            dim (int): Input and output dimensionality.
            inter_dim (int): Hidden layer dimensionality.
        """
        super().__init__()
        self.w1 = Linear(dim, inter_dim)
        self.w2 = Linear(inter_dim, dim)
        self.w3 = Linear(dim, inter_dim)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        Forward pass for the Expert layer.

        Args:
            x (torch.Tensor): Input tensor.

        Returns:
            torch.Tensor: Output tensor after expert computation.
        """
        return self.w2(F.silu(self.w1(x)) * self.w3(x))

最后得到MoE代码如下：

class MoE(nn.Module):
    """
    Mixture-of-Experts (MoE) module.

    Attributes:
        dim (int): Dimensionality of input features.
        n_routed_experts (int): 模型中总的专家数量
        n_local_experts (int): 在分布式系统中，当前设备（节点）负责的专家数量
        n_activated_experts (int): 每个输入激活的专家数量（即每个输入会被路由到多少个专家）。
        gate (nn.Module): Gating mechanism to route inputs to experts.
        experts (nn.ModuleList): List of expert modules.
        shared_experts (nn.Module): Shared experts applied to all inputs.
    """
    def __init__(self, args: ModelArgs):
        """
        Initializes the MoE module.

        Args:
            args (ModelArgs): Model arguments containing MoE parameters.
        """
        super().__init__()
        self.dim = args.dim
        assert args.n_routed_experts % world_size == 0
        self.n_routed_experts = args.n_routed_experts
        self.n_local_experts = args.n_routed_experts // world_size
        self.n_activated_experts = args.n_activated_experts

        # 起始/结束（因为是涉及到分布训练，去寻找每个设备上的”专家“即可）
        self.experts_start_idx = rank * self.n_local_experts
        self.experts_end_idx = self.experts_start_idx + self.n_local_experts
        
        self.gate = Gate(args)
        self.experts = nn.ModuleList([Expert(args.dim, args.moe_inter_dim) if self.experts_start_idx <= i < self.experts_end_idx else None
                                      for i in range(self.n_routed_experts)])
        self.shared_experts = MLP(args.dim, args.n_shared_experts * args.moe_inter_dim)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        Forward pass for the MoE module.

        Args:
            x (torch.Tensor): Input tensor.

        Returns:
            torch.Tensor: Output tensor after expert routing and computation.
        """
        shape = x.size()
        x = x.view(-1, self.dim)
        weights, indices = self.gate(x)
        y = torch.zeros_like(x)
        counts = torch.bincount(indices.flatten(), minlength=self.n_routed_experts).tolist()
        for i in range(self.experts_start_idx, self.experts_end_idx):
            if counts[i] == 0:
                continue
            expert = self.experts[i]
            idx, top = torch.where(indices == i)
            y[idx] += expert(x[idx]) * weights[idx, top, None]
        z = self.shared_experts(x)
        if world_size > 1:
            dist.all_reduce(y)
        return (y + z).view(shape)

代码分析：
1、获取权重以及索引：weights, indices = self.gate(x)
2、计算每个专家索引：counts = torch.bincount(indices.flatten(), minlength=self.n_routed_experts).tolist()通过torch.bincount返回数值个数，比如说：[1,2,2,2,3]，那么返回：[0,1,3,1]（0出现0次，1出现1次。。。。）相当于对每个专家都编号了，只需要根据出现次数，来索引出来
3、计算加权得分：

for i in range(self.experts_start_idx, self.experts_end_idx):
    if counts[i] == 0:
        continue
    expert = self.experts[i]
    idx, top = torch.where(indices == i)
    y[idx] += expert(x[idx]) * weights[idx, top, None]

3、平衡不同专家之间的负载

如果涉及到多个专家，很可能就会出现一种情况：只有部分的专家被使用进而导致负载不均衡。那么可以通过 负载均衡损失（Load Balancing Loss）计算主要为：
1、importance loss（重要性损失）
回到上面对于router函数（$s = \text{softmax}(W_{gate}x+b)$）在论文中对于重要性损失定义如下：

路由器函数为：$s = \text{Softmax}(\text{TopK}(W_{gate}x+n, k))$，区别在于补充一个高斯分布的$n$，以及选择TopK个路由器然后再去通过softmax进行处理（因为选择TopK这样一来其他的都是负无穷在通过softmax处理之后值为0）
在DeepSeek V-3里面也是这样操作的，选择TopK

\[L_{importance}(x)=(\frac{\text{std(x)}}{\text{mean}(x)})^2\]

也就是说，通过最小化上式子的最小值（均值大，方差小），进而保证所有的专家平均而言拥有相似的权重。

2、Load Loss：重要性损失旨在保证所有专家平均而言具有相似的路由权重。但是不难想到这些看上去有着总体趋于平衡的权重的路由配置，仍然有一小部分专家获得了所有分配，如下图：

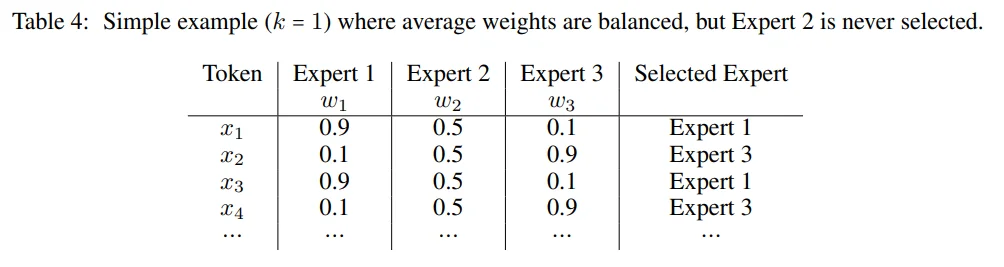
首先，对于专家选择阈值：$threshold_k(x):= max_k(Wx+ \phi)$，其中$\phi$代表前向传播过程中的采样噪声，$max_k$代表选择第$k$个最大的值，对于专家的负载：指的是在整个批次中的使用情况：$load_i(X)=\sum_{x\in X}p_i(x)$对于这个概率的计算：

\[p_i(x):=P(\phi_{new}≥threshold_k(x)-(Wx)_i)\]

其中$\phi_{\mathrm{new}}\sim\mathcal{N}(0,\sigma^{2}),\sigma=1/E$最后对于load loss定义为：

\[L_{load}(X)=(\frac{std(load(X))}{mean(load(X))})^2\]

最后损失函数为：$L=\frac{1}{2}L_{importance}(X)+ \frac{1}{2}L_{load}(X)$

---

借鉴这部分描述对于load balancing loss描述

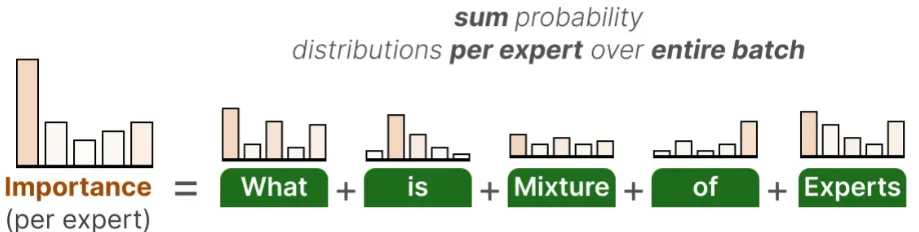
对于每个文本都会选择一个专家模型进行输入，因此都会通过路由器去计算他们的“得分”，去将这部分得分加起来，然后最小化$L_{load}(X)=(\frac{std(load(X))}{mean(load(X))})^2$这部分损失

DeepSeek v3处理负载不均衡问题：在常规的路由器处理得到：

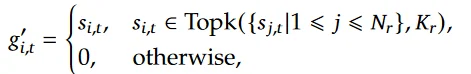
在DeepSeek中通过不同一个“动态调节”参数：$b_i$来保证不同专家之间的负载平衡

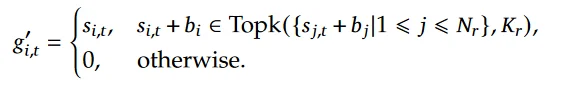
具体实现方法（参考论文：https://arxiv.org/pdf/2408.15664中的描述）：

---

同时也可以采用另外的方法：
1、GShard设定一个 专家容量：设定一个阈值，定义一个专家能处理多少令牌。如果两个专家的容量都达到上限，令牌就会溢出，并通过残差连接传递到下一层，或在某些情况下被完全丢弃。对于专家容量可以借鉴下面处理方式：$\frac{\text{tokens per batch}}{\text{number of experts}}\times \text{capacity factor}$（$\text{capacity factor}$可以选择1-1.25之间）

KV cache

Transformer模型推理过程为：

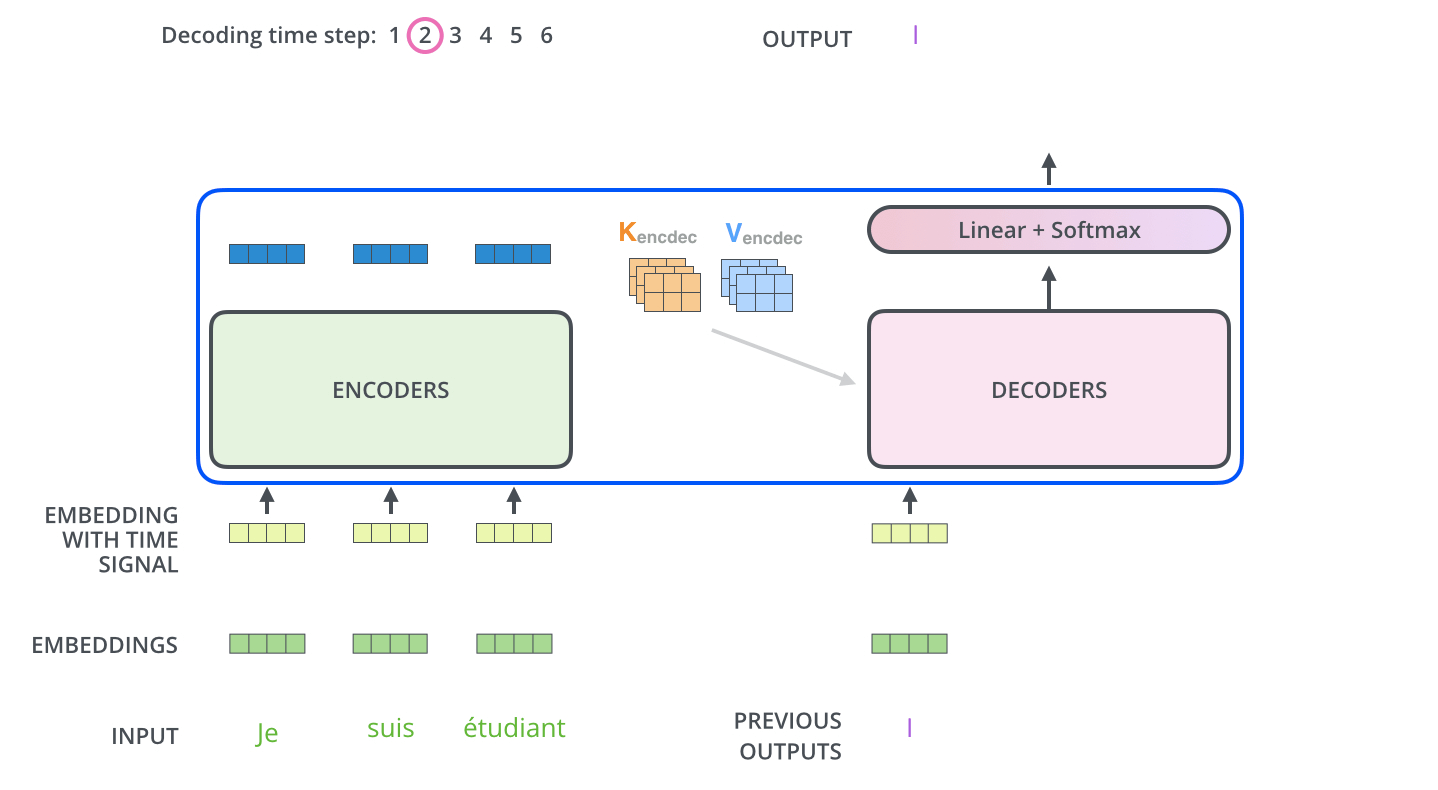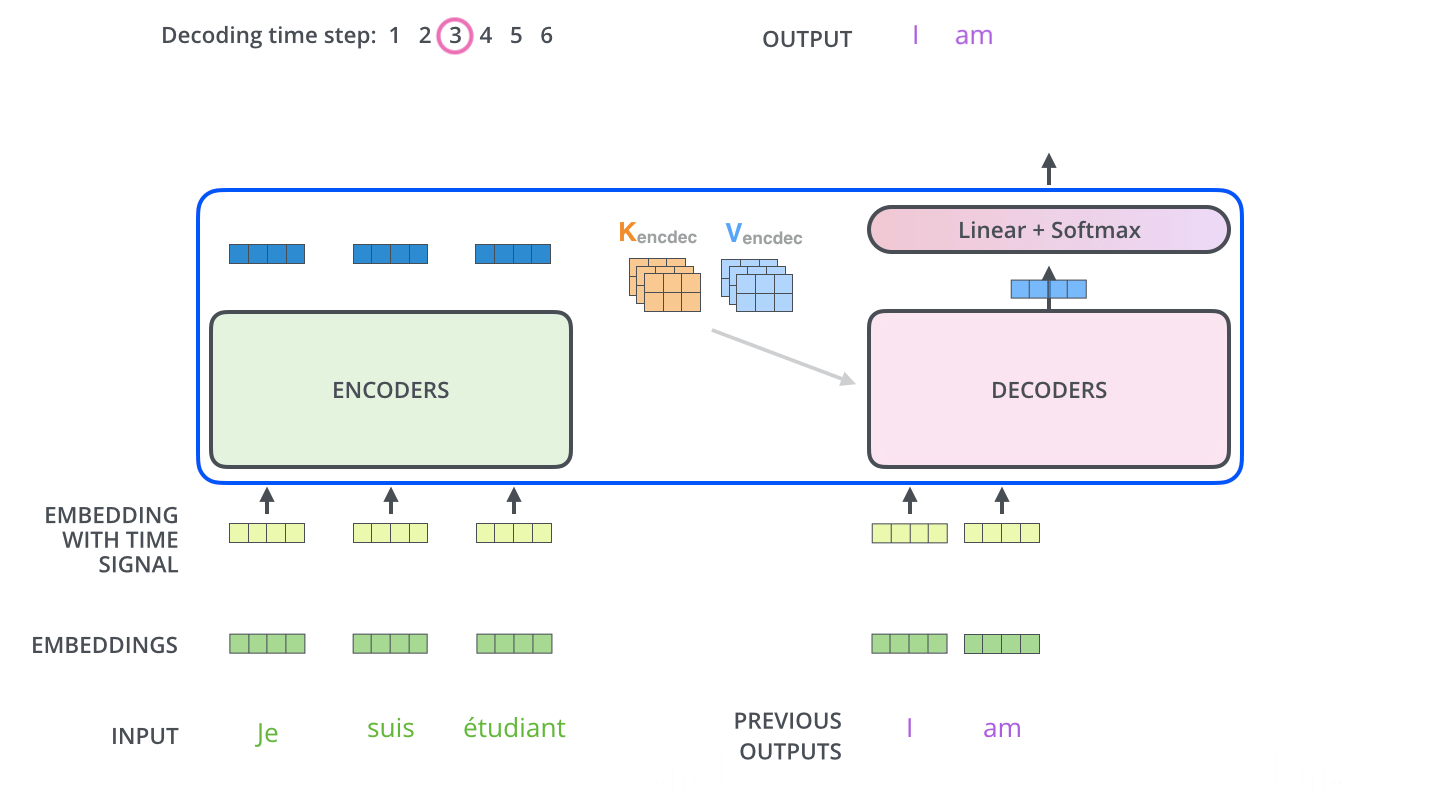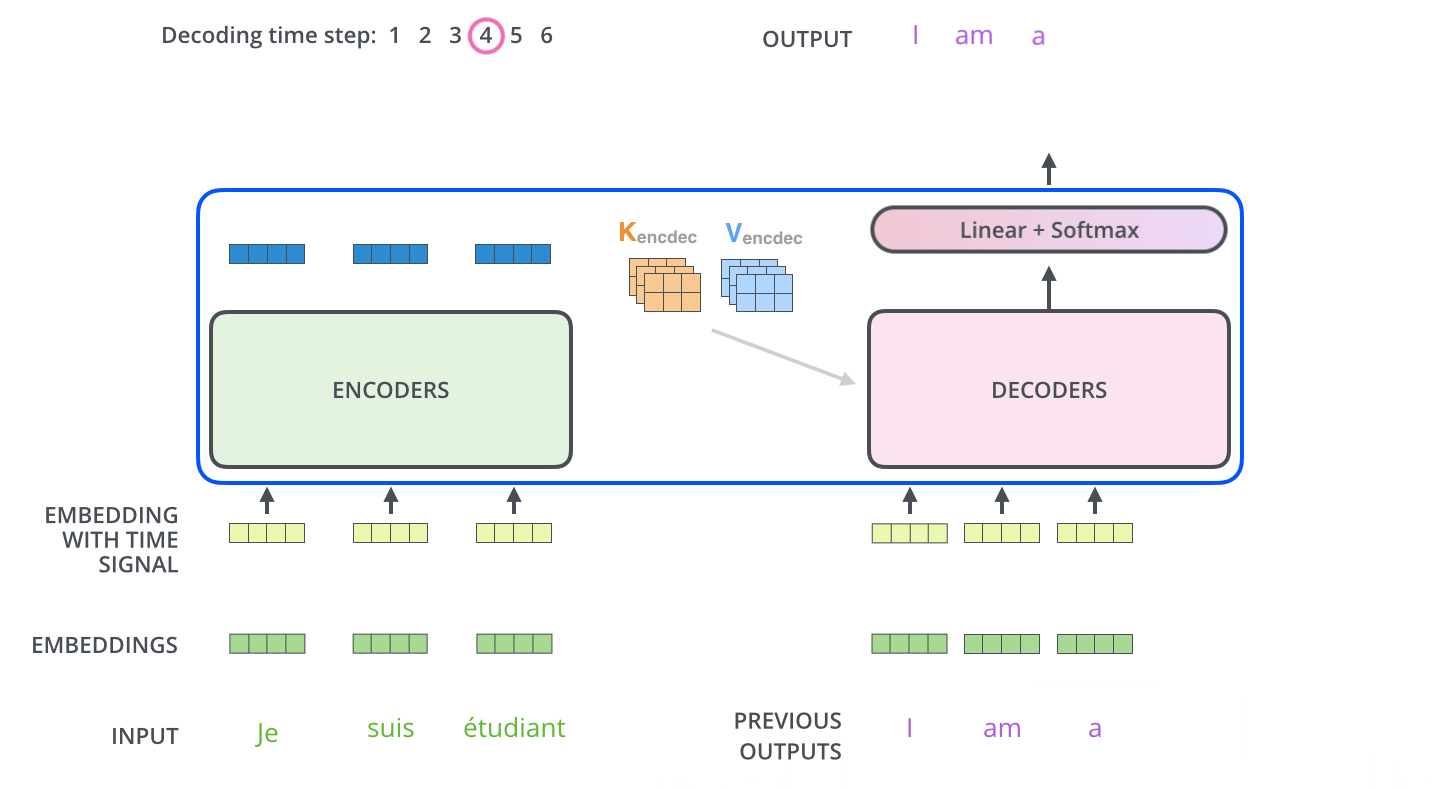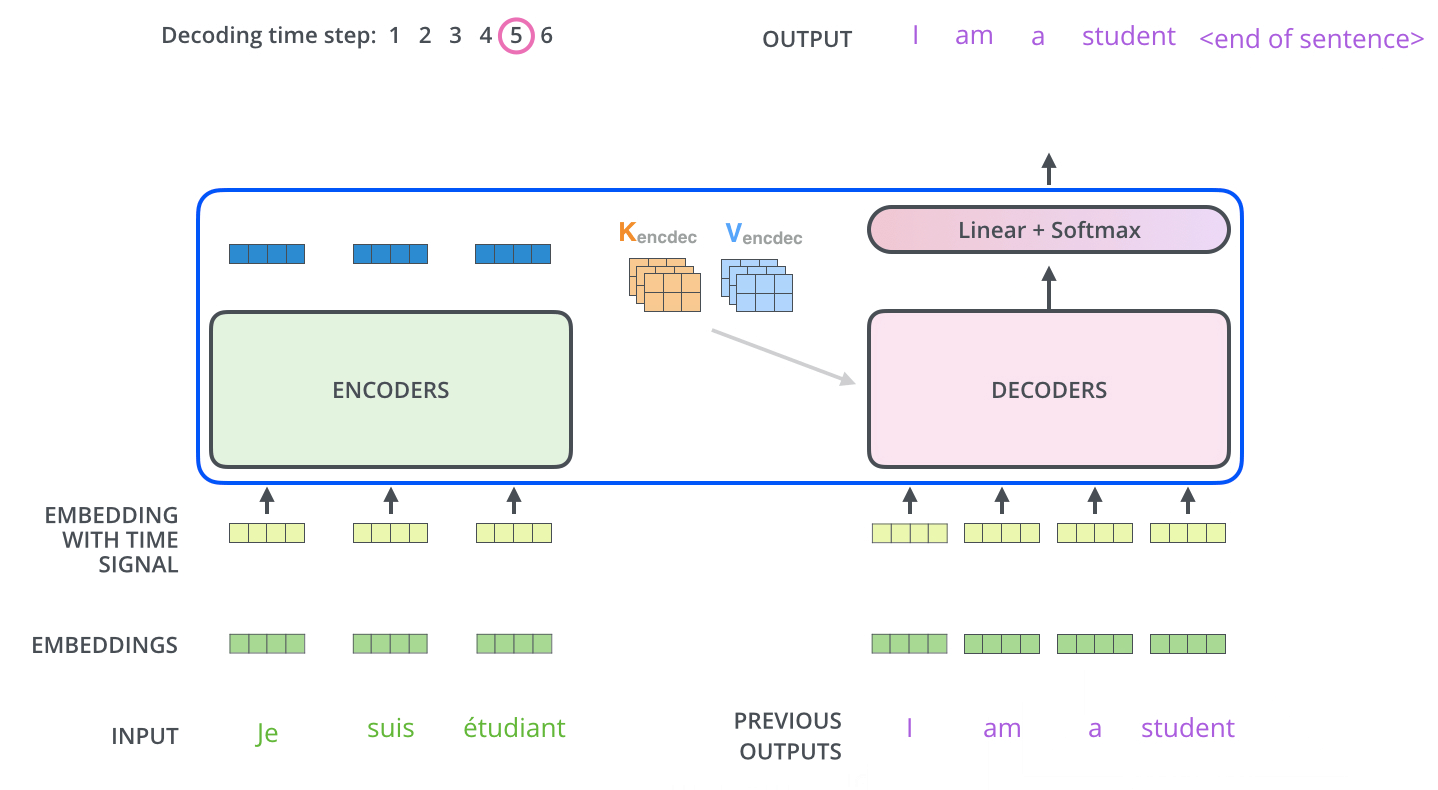
目前主流的LLM框架主要都是使用的decoder-only（也就是说只用Transformer中的decoder结构）

对于LLM任务（通常采用自回归过程）可以简单认为是一种“完形填空”的过程，在输入前面i-1个词然后推测第i个词

回归上面的推理过程（翻译输出：i am a student）：模型中在输出’a’的时候会将’i am’都输入到模型中。理解这个过程（假设就是直接输出文本：i am a student）：

参考：https://zhuanlan.zhihu.com/p/662498827

step1: in: Q=K<S> || out: i
$Attention_1: Q_1K_1^T$
step2: in: Q=K=<s>,i || out: i am
$Attention_1: Q_1K_1^T \ Attention_2:Q_2K_1^T, Q_2K_2^T$
step3: in: Q=K=<s>, i, am || out: i am a
$Attention_1: Q_1K_1^T \ Attention_2:Q_2K_1^T, Q_2K_2^T \
Attention_3: Q_3K_1^T, Q_3K_2^T, Q_3K_3^T$
step4: in: Q=K=<s>, i, am, a || out: i am a student
$Attention_1: Q_1K_1^T \ Attention_2:Q_2K_1^T, Q_2K_2^T \
Attention_3: Q_3K_1^T, Q_3K_2^T, Q_3K_3^T \
Attention_4: Q_4K_1^T, Q_4K_2^T, Q_4K_3^T, Q_4K_4^T
$

不过上面操作过程中会有问题：
计算有很大冗余（每次生成新的词，都需要回归一下之前生成的词），并且每次计算$Attention_i$只与$Q_i$相关对于后面一点理解（以step2为例）：
我目前已经有两个$Q$：$Q_1$:<s>, $Q_2:\text{i}$。并且还有K和V（这两个也是有两个值），我会初始化一个$Q_3$对于下一个值我就用$Q_3$进行表示，然后我就需要去计算注意力得分（只用Q,K,V这三个值计算过程举例）：
$QK^T=(bs, 3, embed_dim)(bs, embed_dim, 2)=(bs, 3, 2)$，接下来计算$QK^TV=(bs, 3, 2)(bs,2,embed_dim)=(bs, 3, embed_dim)$
那么在这个过程中就会有一个有意思问题：Q会有重复的（dim=3，前面两个都是前面已经计算过的）（观察上面Attention计算可以发现:每次计算$Attention_i$只与$Q_i$相关）。因此就有KV-cache理论：既然每次都是Q在变化，但是K和V都是用的之前的，那我之前每次就只用新的Q去和旧的KV计算即可（将KV存储起来），KV-cache一种典型的用内存换速度的方法。

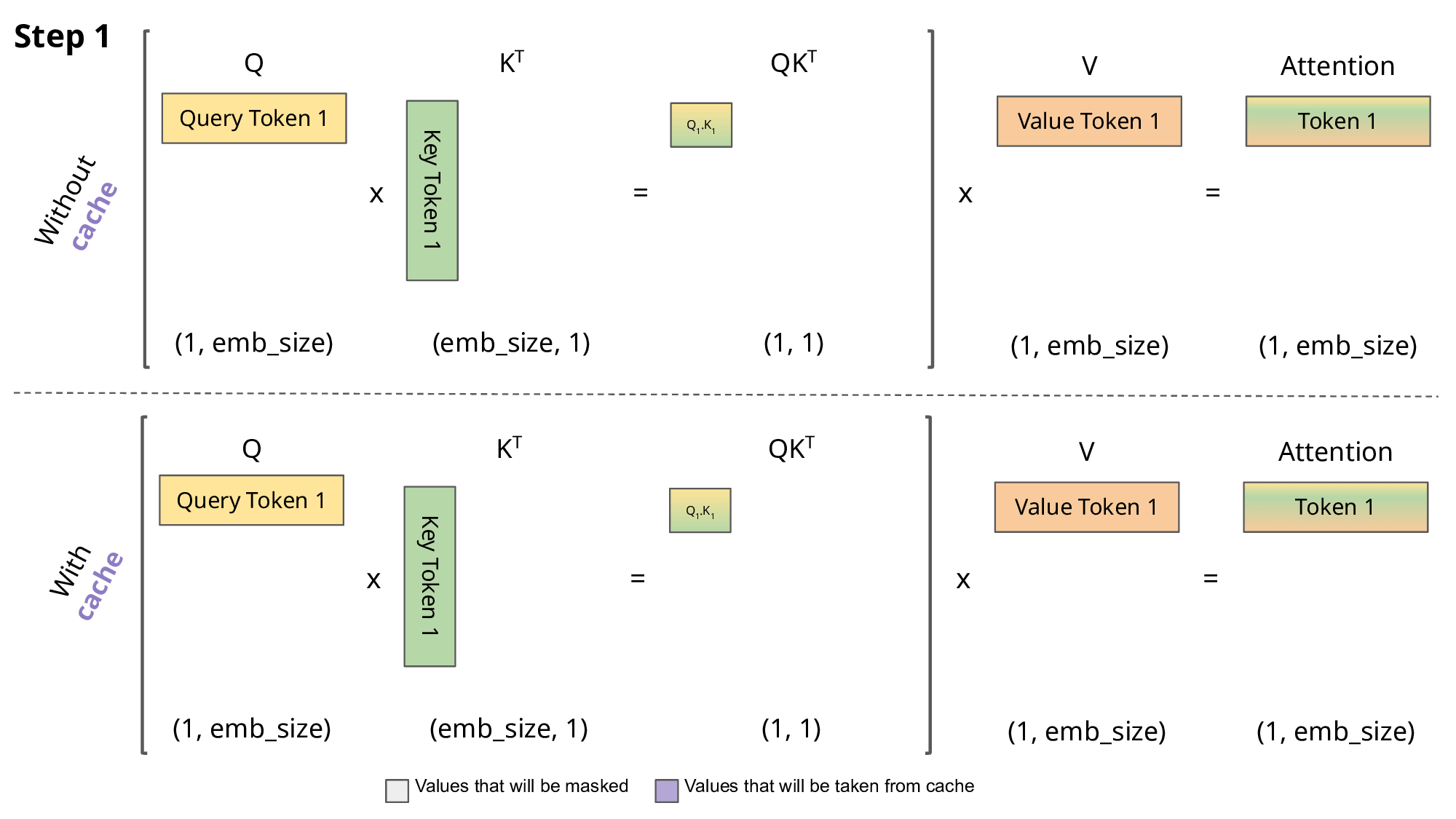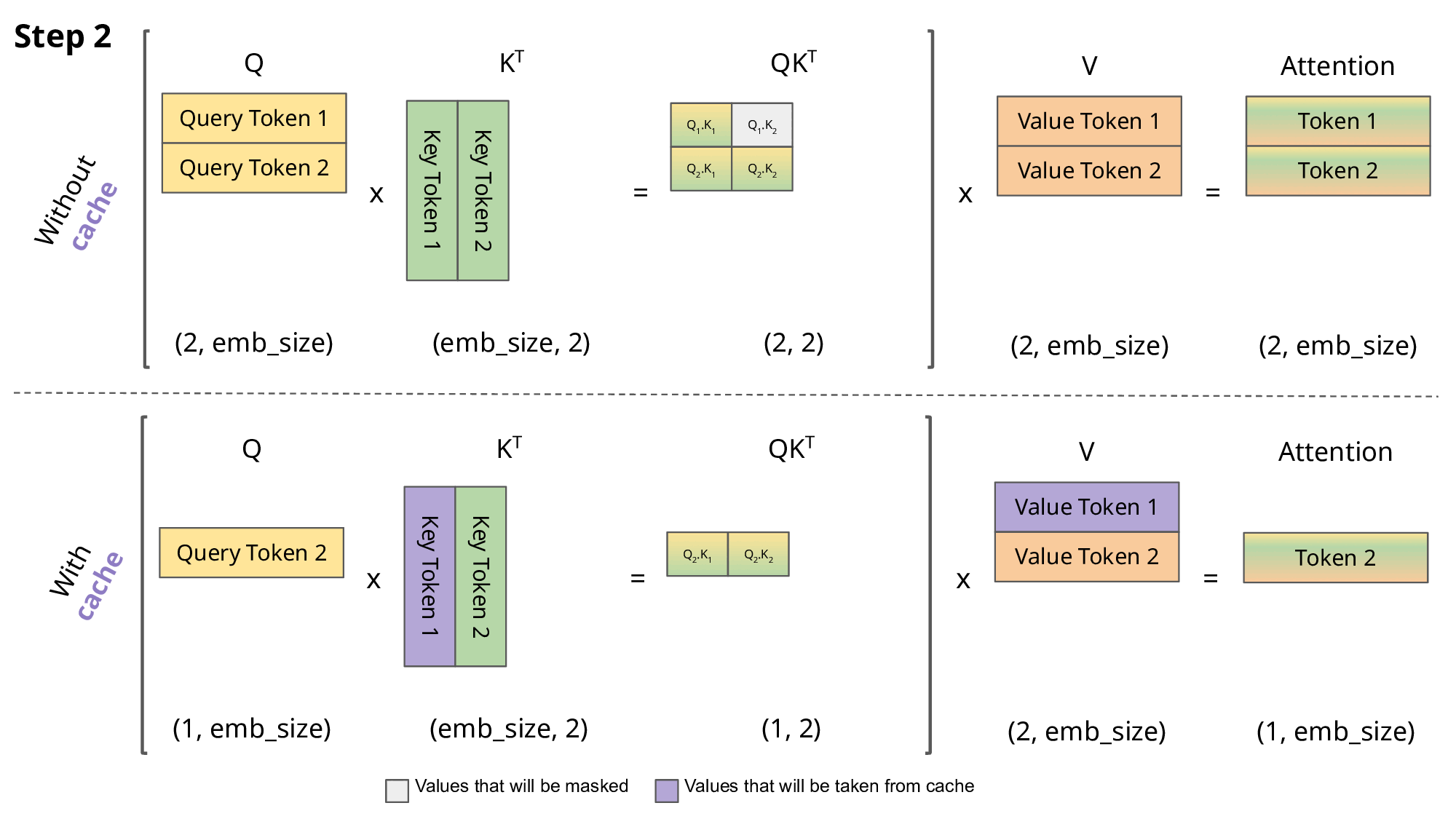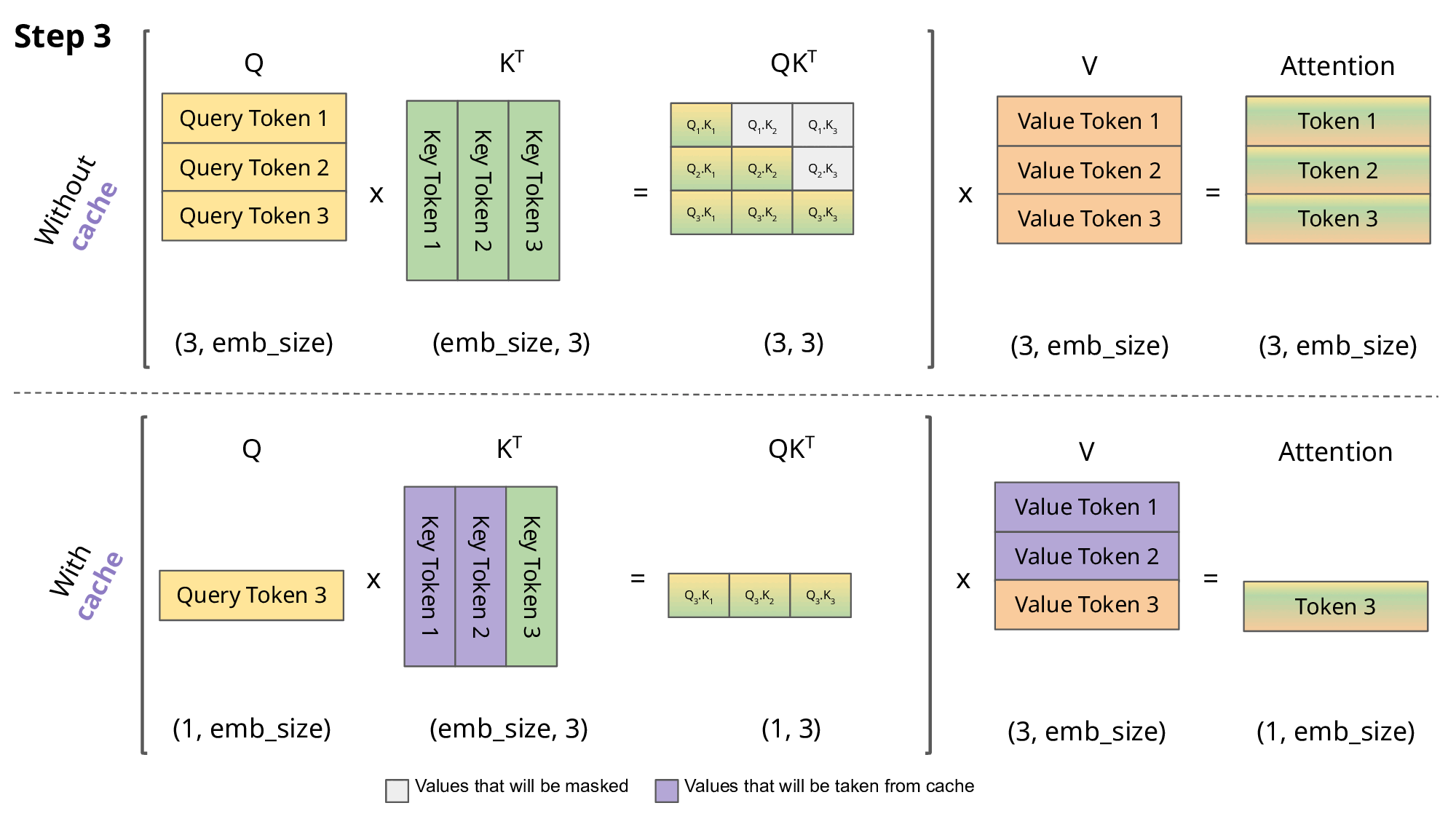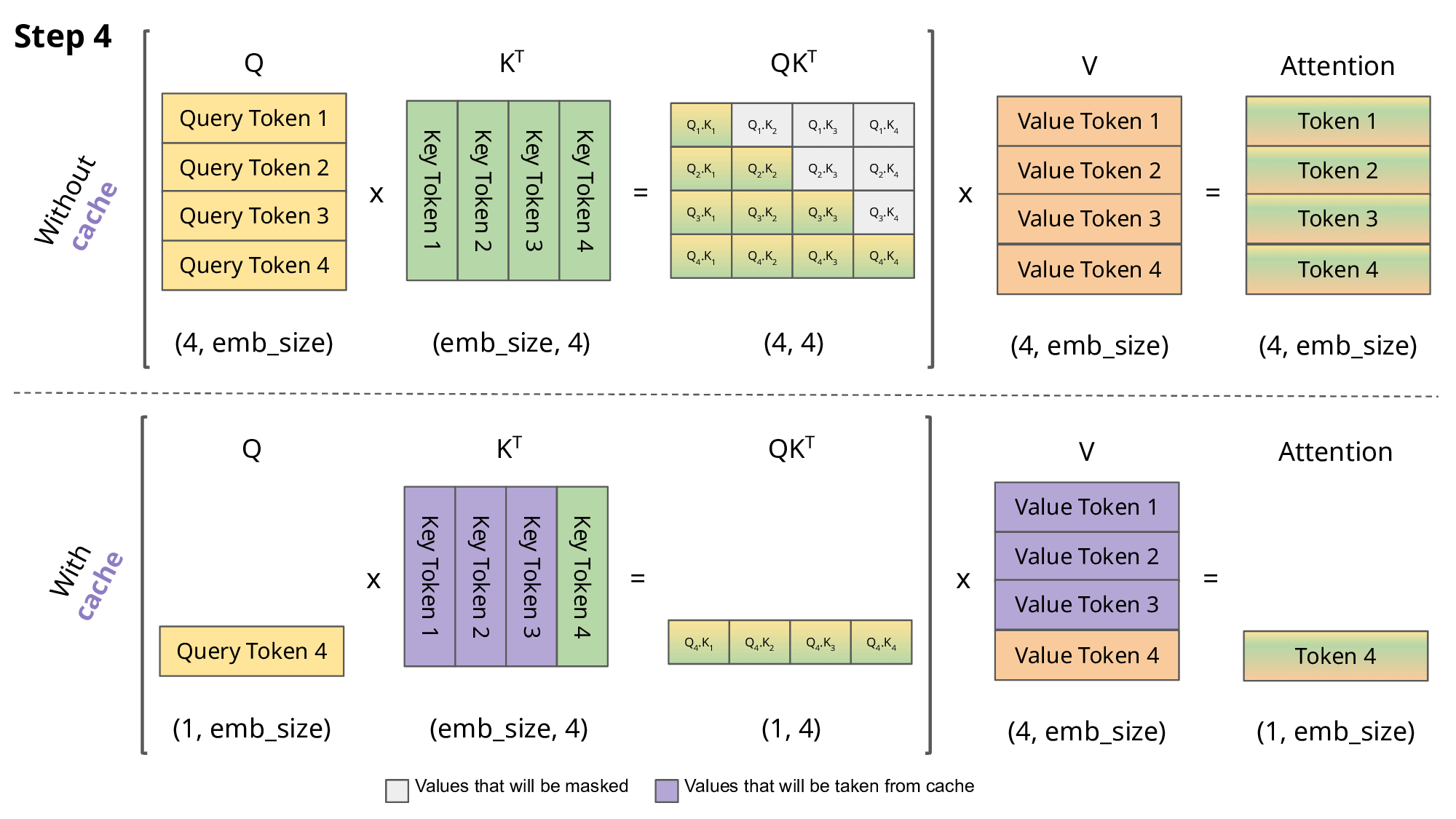
对于KV-cache更加直接的了解：对于模型的新的输出只与最后一个token有关，那么计算过程中没必要将之前的值再拿出来再计算一遍。而q是由输入数据动态计算出来的，而k，v是历史状态因此只会去缓存KV。

简易Demo:

import torch

class KVCache:
    def __init__(self):
        self.k = None
        self.v = None

    def update(self, k, v):
        if self.k is None:
            self.k = k
            self.v = v
        else:
            self.k = torch.cat([self.k, k], dim=1)  # 在序列维度上拼接
            self.v = torch.cat([self.v, v], dim=1)

    def get(self):
        return self.k, self.v

class Decoder(torch.nn.Module):
    def __init__(self, embed_dim, hidden_dim, vocab_size, num_heads=8):
        super().__init__()
        self.embedding = torch.nn.Embedding(vocab_size, embed_dim)
        self.attention = torch.nn.MultiheadAttention(embed_dim, num_heads)
        self.linear = torch.nn.Linear(embed_dim, vocab_size)
        self.kv_cache = KVCache()

    def forward(self, input_ids):
        x = self.embedding(input_ids)  # (batch_size, seq_len, embed_dim)

        # 获取 KV-cache
        k, v = self.kv_cache.get()

        # 计算 Attention
        if k is not None and v is not None:
            # 使用 KV-cache
            attn_output, _ = self.attention(x, k, v)  # (batch_size, seq_len, embed_dim)
        else:
            # 初始状态，没有 KV-cache
            attn_output, _ = self.attention(x, x, x)  # (batch_size, seq_len, embed_dim)

        # 更新 KV-cache
        self.kv_cache.update(x, x)

        # 残差连接
        x = x + attn_output

        # 线性变换
        logits = self.linear(x)  # (batch_size, seq_len, vocab_size)

        return logits

batch_size = 2
seq_len = 4
embed_dim = 64
hidden_dim = 256
vocab_size = 10000  # 假设词汇表大小为 10000
decoder = Decoder(embed_dim, hidden_dim, vocab_size)
input_ids = torch.randint(0, vocab_size, (batch_size, seq_len))  # (batch_size, seq_len)
logits = decoder(input_ids)  # (batch_size, seq_len, vocab_size)
print("Logits shape:", logits.shape)

使用Huggingface的transformers框架代码：https://huggingface.co/docs/transformers/main/en/kv_cache。只需要类似下面操作：

import torch
from transformers import AutoTokenizer, AutoModelForCausalLM
ckpt = "microsoft/Phi-3-mini-4k-instruct"

tokenizer = AutoTokenizer.from_pretrained(ckpt)
model = AutoModelForCausalLM.from_pretrained(ckpt, torch_dtype=torch.float16).to("cuda:0")
inputs = tokenizer("Fun fact: The shortest", return_tensors="pt").to(model.device)

# 具体参数：https://huggingface.co/docs/transformers/en/main_classes/text_generation
out = model.generate(**inputs, do_sample=False, max_new_tokens=23, use_cache=True)
print(tokenizer.batch_decode(out, skip_special_tokens=True)[0])

out = model.generate(**inputs, do_sample=False, max_new_tokens=23)
print(tokenizer.batch_decode(out, skip_special_tokens=True)[0])

在Transformers中不同cache方式：

缓存类型	描述	适用场景	优点	缺点
StaticCache	静态缓存，缓存所有的 K 和 V，不更新。	短序列生成、内存充足的场景	实现简单，快速	不适合长序列生成，内存消耗较大
OffloadedStaticCache	静态缓存，但将缓存内容卸载到外部存储。	内存受限的环境，长序列生成	减少显存占用，适合大规模生成	存取速度较慢，可能影响生成速度
SlidingWindowCache	滑动窗口缓存，缓存一个固定大小的窗口。	长序列生成、内存有限的场景	限制内存消耗，适合长序列生成	窗口太小可能丢失上下文信息，影响生成效果
HybridCache	混合缓存，结合静态缓存和滑动窗口缓存。	长序列生成，要求平衡内存和上下文	平衡内存消耗和上下文保留	比静态缓存更复杂，可能需要更多内存管理和计算资源
MambaCache	高效的缓存实现，针对推理速度和内存占用进行了优化。	高性能计算环境、高并发推理任务	高度优化，适合大规模并行推理	可能需要特定硬件支持，复杂度较高
QuantizedCache	量化缓存，减少存储需求。	内存受限的设备、需要减少内存占用的场景	大幅度减少内存占用，适合嵌入式设备	量化可能导致精度损失，影响生成质量

争对上面描述其实KV-cahce是一种用存储换速度的方法，因此，对于KV存储进行优化就十分有必要了！对于KV-cache存储优化可以参考文章。

结论

主要介绍了MoE以及KV-cache理论及其代码，前者是将传统的mlp替换为：通过一个路由器将输入x就行选择，然后传入不同的专家模型（mlp）。后者则是对于计算attention过程中将中间过程值：KV进行缓存，这是因为模型新的输出只与最后一个输出的token有关，然后q是动态变化的因此只会去缓存kv

参考

1、https://arxiv.org/pdf/2101.03961
2、混合专家模型 (MoE) 详解
3、https://arxiv.org/pdf/2407.06204
4、https://github.com/deepseek-ai/DeepSeek-V3/blob/main/inference/model.py
5、https://arxiv.org/pdf/2106.05974
6、https://arxiv.org/pdf/2006.16668
7、https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdf
8、https://jalammar.github.io/illustrated-transformer/
9、https://zhuanlan.zhihu.com/p/662498827
10、https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-mixture-of-experts
11、https://arxiv.org/pdf/2412.19437
12、https://arxiv.org/pdf/2408.15664