深度学习基础理论————学习率优化方法(AdaGrad/RMSprop/Adam/Warm-UP)-Big-Yellow-J

学习率基础¹

学习率（Learning Rate）在优化算法，尤其是梯度下降和其变体中，扮演着至关重要的角色。它影响着模型训练的速度和稳定性，并且是实现模型优化的关键参数之一。

如何理解呢？

在统计学中，线性方程的优化过程通常包括以下步骤：

构建方程：定义一个模型，例如线性方程 $y = wx + b$。
定义损失函数：选择一个衡量模型预测值与真实值差异的函数，通常是最小二乘法，即最小化误差平方和。
参数计算：通过最小二乘法计算方程中的参数 $w$ 和 $b$，使得损失函数最小。

深度学习中的优化操作
对于深度学习，这个过程是类似的，但更为复杂：

假设我们定义的模型为 $f(x)$，其中参数为 $\theta$。
计算得到的预测值为 $\hat{y}$，真实值为 $y$。
我们定义损失函数为 $Loss = \sum(\hat{y} - y)^2$（损失函数也可以选择其他的）。

如何优化损失函数
那么，如何去优化这个损失函数呢？这里可以考虑以下问题：

回归问题：以回归为例，预测值和真实值应该是不断接近的，也就是说，损失值是不断减小的。

步骤详解

计算梯度：首先，我们需要计算损失函数相对于模型参数 $\theta$ 的梯度。这个梯度告诉我们在参数空间中哪个方向可以使损失函数减少。在深度学习中，这通常是通过反向传播算法（Backpropagation）来完成的。

这里可以考虑类似小球从山上滚下来，我知道了小球滚到底部的方向（梯度）但是我要小球快速的滚到山底，那么我就可以给他加一个“速度”也就是学习率，这样一来优化过程变成：$\theta_{new}=\theta_{old}- \alpha \times \nabla J(\theta_{old})$

选择优化算法：有了梯度之后，我们需要一个优化算法来更新模型的参数。常用的优化算法包括梯度下降（Gradient Descent）、随机梯度下降（SGD）、小批量梯度下降（Mini-batch Gradient Descent）、Adam、RMSprop 等。这些算法的主要区别在于它们如何处理梯度和更新参数。
参数更新：使用优化算法，我们根据梯度和学习率来更新模型的参数。学习率是一个超参数，它决定了每次更新参数时的步长。

学习率与梯度下降
学习率在不同类型的梯度下降算法中有不同的应用和解释。最常见的三种梯度下降算法是：

批量梯度下降（Batch Gradient Descent）
随机梯度下降（Stochastic Gradient Descent, SGD）
小批量梯度下降（Mini-batch Gradient Descent）
在批量梯度下降中，学习率应用于整个数据集，用于计算损失函数的平均梯度。而在随机梯度下降和小批量梯度下降中，学习率应用于单个或一小批样本，用于更新模型参数。

随机梯度下降和小批量梯度下降由于其高度随机的性质，常常需要一个逐渐衰减的学习率，以帮助模型收敛。

学习率对模型性能的影响
选择合适的学习率是非常重要的，因为它会直接影响模型的训练速度和最终性能。具体来说：

过大的学习率：可能导致模型在最优解附近震荡，或者在极端情况下导致模型发散。
过小的学习率：虽然能够保证模型最终收敛，但是会大大降低模型训练的速度。有时，它甚至可能导致模型陷入局部最优解。
实验表明，不同的模型结构和不同的数据集通常需要不同的学习率设置。因此，实践中常常需要多次尝试和调整，或者使用自适应学习率算法。

学习率调整策略

1、自适应学习率

每个参数的学习率可以根据过去的梯度信息动态调整，而不是使用一个固定的全局学习率

1. AdaGrad

AdaGrad 是一种自适应学习率的优化算法，它通过累积所有梯度的平方来调整每个参数的学习率。AdaGrad 的更新规则如下：
$\mathbf{g}_t = \mathbf{g}_{t-1} + \nabla_{\theta} J(\theta_t) \odot \nabla_{\theta} J(\theta_t)$
$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\mathbf{g}_t + \epsilon}} \odot \nabla_{\theta} J(\theta_t)$

其中，$\eta$ 是全局学习率，$\epsilon$ 是为了防止除零而添加的一个小常数，$\odot$ 表示元素级的乘法。

2. RMSprop

RMSprop 是另一种自适应学习率的优化算法，它使用梯度的指数加权移动平均值来调整每个参数的学习率。RMSprop 的更新规则如下：
$\mathbf{s}_t = \rho \mathbf{s}_{t-1} + (1 - \rho) \nabla_{\theta} J(\theta_t) \odot \nabla_{\theta} J(\theta_t)$
$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \odot \nabla_{\theta} J(\theta_t)$

其中，$\rho$ 是梯度平方的衰减率，$\eta$ 是全局学习率，$\epsilon$ 是为了防止除零而添加的一个小常数。

3. Adam

Adam 结合了 Momentum 和 RMSprop 的优点，使用梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率。Adam 的更新规则如下：
$\mathbf{m}_t = \beta_1 \mathbf{m}_{t-1} + (1 - \beta_1) \nabla_{\theta} J(\theta_t)$
$\mathbf{v}_t = \beta_2 \mathbf{v}_{t-1} + (1 - \beta_2) \nabla_{\theta} J(\theta_t) \odot \nabla_{\theta} J(\theta_t)$
$\hat{\mathbf{m}}_t = \frac{\mathbf{m}_t}{1 - \beta_1^t}$
$\hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_2^t}$
$\theta_{t+1} = \theta_t - \eta \frac{\hat{\mathbf{m}}_t}{\sqrt{\hat{\mathbf{v}}_t + \epsilon}}$

其中，$\beta_1$ 和 $\beta_2$ 分别是一阶和二阶矩估计的衰减率，$\eta$ 是全局学习率，$\epsilon$ 是为了防止除零而添加的一个小常数。

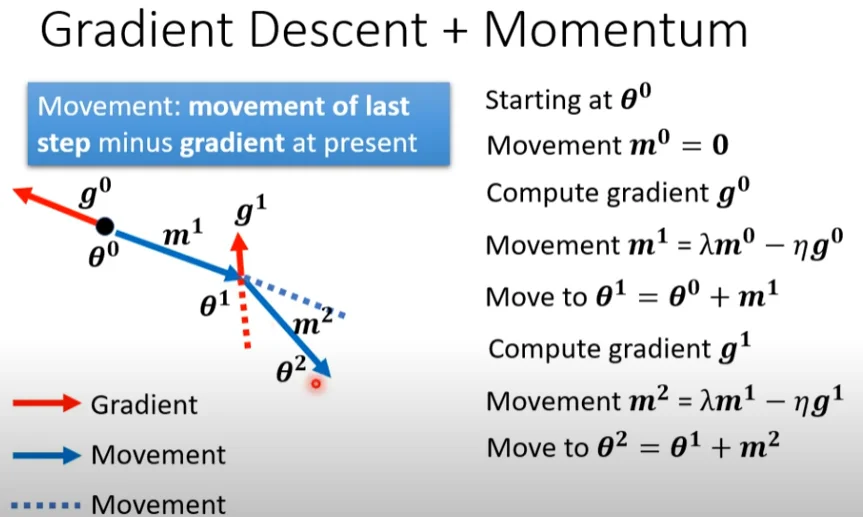
动量方法：深度学习参数的优化不只考虑本次的梯度方向还要去考虑上一次的梯度方向²

初始化动量为0从$\theta_0$到$\theta_1$因为动量为0，那么就直接走梯度方向，从$\theta_1$到$\theta_2$此时就有动量了，不只是走本次的梯度方向（$g^1$）还要考虑上一次的$m^2$因此对两个叠加得到新的方向：$\theta^2$
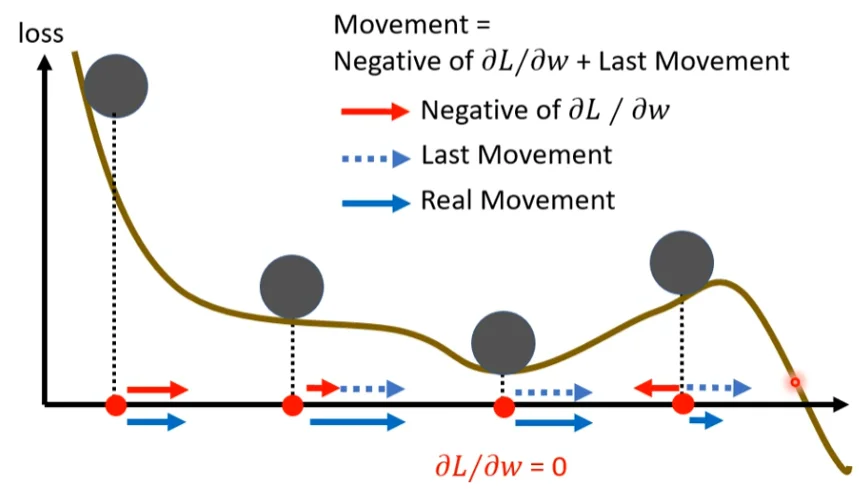
动量方法如何起作用：

通过考虑前面的梯度避免陷入“鞍点”

学习率调整其他策略

1、warm-up

在深度学习模型训练中，使用较小的学习率进行warm up操作的原理是为了让模型逐渐适应数据集的特征，避免模型在训练开始时出现过拟合或欠拟合的情况。同时，由于较小的学习率可以使得模型的权重更新更加平稳，减少了训练时的震荡和不稳定性，从而提高了模型的训练效果。
具体来说，warm up 的作用可以分为以下几个方面：

适应数据集特征：在训练开始时，模型的权重是随机初始化的，如果直接使用较大的学习率进行训练，模型容易出现过拟合或欠拟合的情况。而使用较小的学习率进行warm up操作，可以让模型逐渐适应数据集的特征，减少过拟合或欠拟合的风险。
减少训练震荡：在训练开始时，模型的权重更新可能比较剧烈，导致训练时出现震荡和不稳定性。而使用较小的学习率进行warm up操作，可以使得模型的权重更新更加平稳，减少训练时的震荡和不稳定性。
提高训练效果：通过warm up操作，模型可以逐渐适应数据集的特征，减少过拟合或欠拟合的风险，同时减少训练时的震荡和不稳定性，从而提高模型的训练效果。

实现方法一：

def decay_lr_poly(base_lr, epoch_i, batch_i, total_epochs, total_batches, warm_up, power=1.0):
    '''
    base_lr: 初始化学习率
    epoch_i, batch_i, total_epochs, total_batches: 第i次epoch/batch;总共的epoch/batch
    warm_up: 训练到多少轮次，才变成开始设定学习率
    '''
    if warm_up > 0 and epoch_i < warm_up:
        rate = (epoch_i * total_batches + batch_i) / (warm_up * total_batches)
    else:
        # 学习率衰减
        rate = np.power(
            1.0 - ((epoch_i - warm_up) * total_batches + batch_i) / ((total_epochs - warm_up) * total_batches),
            power)
    return rate * base_lr
...
batch_lr = decay_lr_poly(conf.lr, epoch, batch_i, conf.epochs, batches, conf.warm_up, conf.power)
for group in optimizer.param_groups:
      group['lr'] = batch_lr

实现方法二：

class GradualWarmupScheduler(_LRScheduler):
    def __init__(self, optimizer, total_epochs, warmup_epochs, last_epoch=-1):
        if not isinstance(optimizer, optim.Optimizer):
            raise TypeError('{} is not an Optimizer'.format(
                type(optimizer).__name__))
        self.total_epochs = total_epochs
        self.warmup_epochs = warmup_epochs
        self.base_lrs = [group['lr'] for group in optimizer.param_groups]
        
        super(GradualWarmupScheduler, self).__init__(optimizer, last_epoch)
        
    def get_lr(self):
        if self.last_epoch < self.warmup_epochs:
            return [(self.base_lrs[i] * self.last_epoch / self.warmup_epochs) 
                    for i in range(len(self.base_lrs))]
        return [self.base_lrs[i] for i in range(len(self.base_lrs))]

整个流程代码：

class LinearModel(nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = nn.Linear(10, 1)

    def forward(self, x):
        return self.linear(x)
        
device = 'cuda' if torch.cuda.is_available() else 'cpu'
x = torch.randn(100, 10).to(device)
y = torch.randn(100, 1).to(device)

dataset = TensorDataset(x, y)
dataloader = DataLoader(dataset, batch_size=10, shuffle=True)

model = LinearModel().to(device)
loss_fn = nn.MSELoss()
total_epochs, warmup_epochs, lr = 10, 5, 0.01
optimizer = optim.Adam(model.parameters(), lr=lr)
# 方法2
scheduler = GradualWarmupScheduler(optimizer, total_epochs, warmup_epochs)

for epoch in range(total_epochs):
    model.train()
    for batch_idx, (input, target) in enumerate(dataloader):
        # 方法1
        batch_lr = decay_lr_poly(lr, epoch, batch_idx, total_epochs, len(dataloader), warmup_epochs, 1)
        for group in optimizer.param_groups:
            group['lr'] = batch_lr
        optimizer.zero_grad()
        output = model(input)
        loss = loss_fn(output, target)
        loss.backward()
        optimizer.step()
    # scheduler.step()
    # lr = scheduler.get_lr()[0]
    # print(f'Epoch {epoch+1}, Learning Rate: {lr:.6f}, Loss Value: {loss.item()}')
    print(f'Epoch {epoch+1}, Learning Rate: {batch_lr:.6f}, Loss Value: {loss.item()}')

争对第一种方式选择的优化器有：
1、cosine decay schedule

progress = (epoch_i - warm_up) * total_batches + batch_i
cosine_decay = 0.5 * (1.0 + np.cos(np.pi * progress / ((total_epochs - warm_up) * total_batches)))
rate = cosine_decay

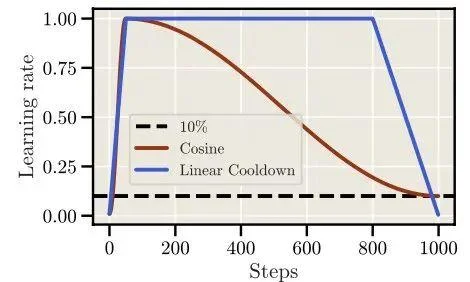
2、Warmup-Stable-Decay³

def decay_lr_stable(base_lr, epoch_i, batch_i, total_epochs, total_batches, warm_up, stable_epochs=0):
    if warm_up > 0 and epoch_i < warm_up:
        # Warmup阶段
        rate = (epoch_i * total_batches + batch_i) / (warm_up * total_batches)
    elif epoch_i < warm_up + stable_epochs:
        # Stable阶段
        rate = 1.0  # 学习率保持为base_lr
    else:
        # Decay阶段
        progress = (epoch_i - warm_up - stable_epochs) * total_batches + batch_i
        cosine_decay = 0.5 * (1.0 + np.cos(np.pi * progress / ((total_epochs - warm_up - stable_epochs) * total_batches)))
        rate = cosine_decay
    return rate * base_lr

实践操作

有时候需要对不同模型做使用不同学习率（比如说多模态中对于Vision-Model和Text-Model）可以这么操作：

optim.SGD([{'params': model.VisionModel.parameters(), 'lr': 1e-2},{'params': model.TextModel.parameters(), 'lr: 1e-3}], lr=1e-3, momentum=0.9)

参考

1:https://cloud.tencent.com/developer/article/2351463
2:https://youtu.be/zzbr1h9sF54?t=1614
3:https://arxiv.org/abs/2404.06395

https://cloud.tencent.com/developer/article/2351463 ↩
https://youtu.be/zzbr1h9sF54?t=1614 ↩
https://arxiv.org/abs/2404.06395 ↩

深度学习基础理论————学习率优化方法(AdaGrad/RMSprop/Adam/Warm-UP)

学习率基础1

学习率调整策略

1、自适应学习率

学习率调整其他策略

实践操作

参考

学习率基础¹