Big-Yellow-J
主要介绍数据蒸馏操作,并且介绍CVPR-2025上海交大满分论文:Dataset Distillation with Neural Characteristic Function: A Minmax Perspective。本文主要是借鉴论文1中的整体结构,大致了解什么是DD而后再去介绍(CVPR-2025)论文。
Data Distillation
数据蒸馏(Data Distillatiob)是一种从大量数据中提取关键信息,生成高质量、小规模合成数据集的技术。它的目标是通过这些合成数据来替代原始数据集,用于模型训练、验证或其他任务,从而提高效率、降低成本或保护隐私。数据蒸馏的核心思想是“从数据中提取数据”,让合成数据集中保留原始数据集的关键特征和分布信息,同时去除冗余和噪声。参考论文1中的描述:
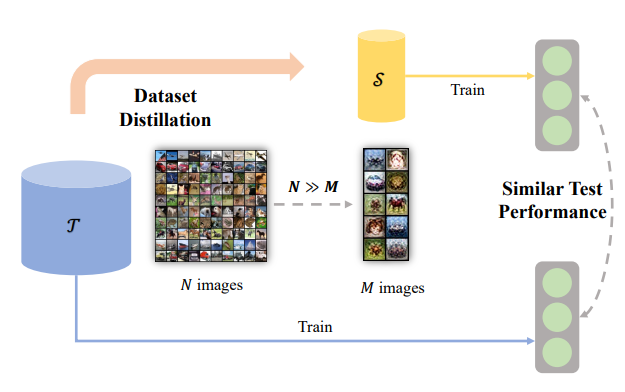
数据蒸馏(DD)目标为:对于一个真实的数据集:$\mathrm{T}=(X_t,Y_t)$ 其中 $X_t\in R^{N\times d}$ 其中 $N$ 代表样本数量 $d$ 代表特征数量,$Y_t\in R^{N\times C}$ 其中$C$为输出实体。对于蒸馏得到的数据集:$\mathrm{S}={X_s,Y_s}$其中$X_s\in R^{M\times D}$其中$M$代表数据蒸馏后的样本数量。最终的优化目标为: $\text{arg min} \mathrm{L}(\mathrm{S}, \mathrm{T})$
比如说对于图像分类任务而言$D$代表的是:HWC而y代表的是独热编码,C代表类别数量

论文1中对于损失函数优化主要分析3种处理思路
1、Performance Matching
\[\begin{aligned} \mathcal{L}(\mathcal{S},\mathcal{T}) & =\mathbb{E}_{\theta^{(0)}\sim\Theta}[l(\mathcal{T};\theta^{(T)})], \\ \theta^{(t)} & =\theta^{(t-1)}-\eta\nabla l(\mathcal{S};\theta^{(t-1)}) \end{aligned}\]其中$\theta, l, T, \eta$分别代表:神经网络参数、损失函数、迭代次数、学习率
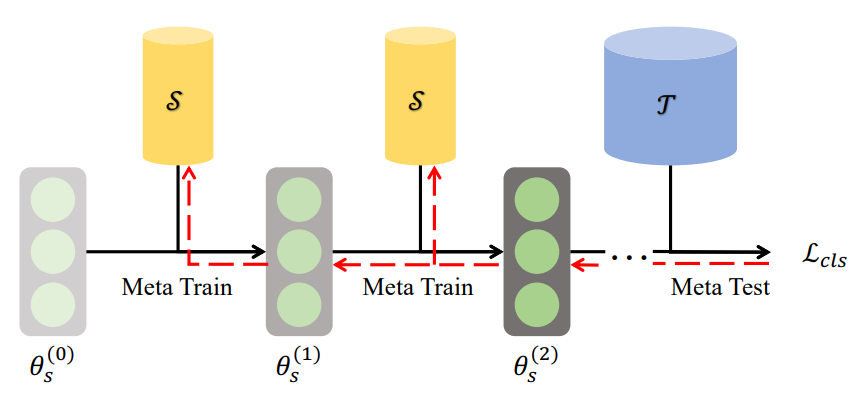
对于上面公式以及优化过程理解:似乎整体优化过程没有体现源数据:$\mathrm{T}$ 和蒸馏数据: $\mathrm{S}$ 两者之间是如何进行优化的,第二个过程直接通过 蒸馏数据去优化梯度,第一个过程则是借助第$T$步得到的参数去计算蒸馏数据集之间差异(这个过程可以理解为模型参数是固定的,但是数据是变化的,需要的是一个数据集在通过源数据集上也有较好的表现)
2、Parameter Matching
分别使用合成数据集和原始数据集对同一个网络进行若干步训练,并促使它们训练得到的神经网络参数保持一致。根据使用合成数据集(S)和原始数据集(T)进行训练的步数,参数匹配方法可以进一步分为两类:单步参数匹配和多步参数匹配。
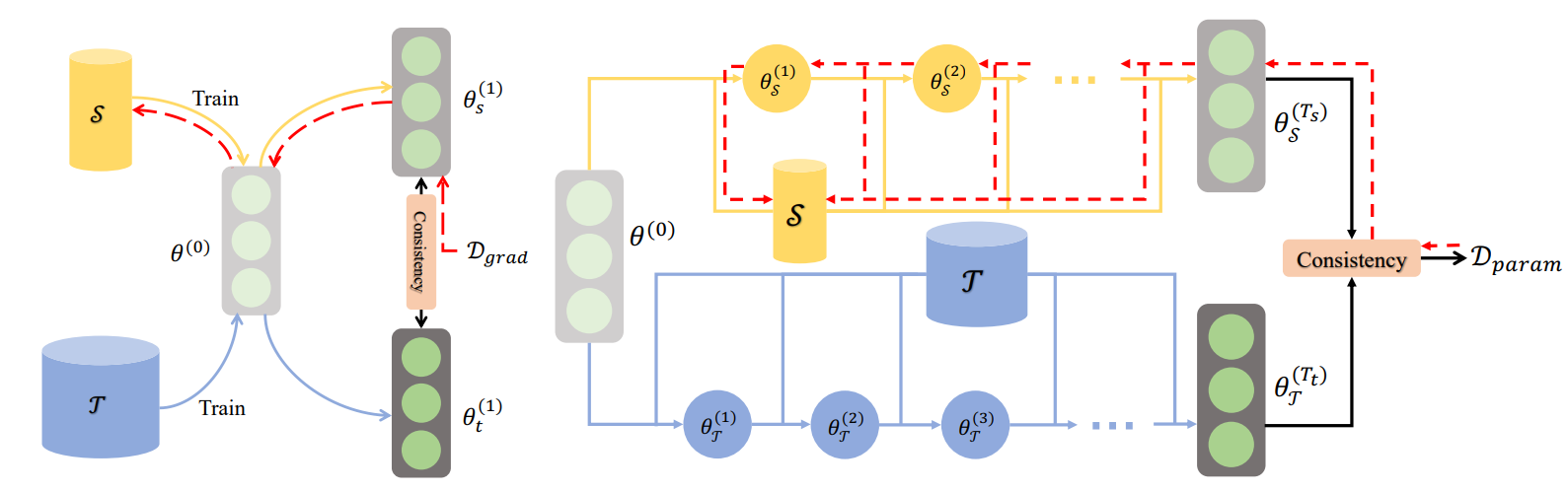
左图为单参数匹配,右图为多参数匹配
- 1、单参数匹配
其中$\mathrm{D}$代表两部分梯度之间的距离
\[\begin{aligned} \mathcal{D}(S, T; \theta) &= \sum_{c=0}^{C-1} d(\nabla l(S_c; \theta), \nabla l(T_c; \theta)), \\ d(A, B) &= \sum_{i=1}^{L} \sum_{j=1}^{J_i} \left(1 - \frac{\mathbf{A}_j^{(i)} \cdot \mathbf{B}_j^{(i)}}{\|\mathbf{A}_j^{(i)}\| \|\mathbf{B}_j^{(i)}\|}\right), \end{aligned}\]- 2、多参数匹配

对于单步参数匹配,由于只匹配单步梯度,因此在评估中可能会积累误差,而模型是通过多步合成数据更新的
\[\begin{aligned} \mathcal{L}(S, T) &= \mathbb{E}_{\theta^{(0)} \sim \Theta} \left[ \mathcal{D}(\theta_S^{(T_s)}, \theta_T^{(T_t)}) \right] \\ \theta_S^{(t)} &= \theta_S^{(t-1)} - \eta \nabla l(S; \theta_S^{(t-1)}) \\ \theta_T^{(t)} &= \theta_T^{(t-1)} - \eta \nabla l(T; \theta_T^{(t-1)}) \\ \mathcal{D}(\theta_S^{(T_s)}, \theta_T^{(T_t)}) &= \frac{\|\theta_S^{(T_s)} - \theta_T^{(T_t)}\|^2}{\|\theta_T^{(T_t)} - \theta^{(0)}\|^2} \end{aligned}\]多步参数则是直接对数据S和T参数进行多步更新,优化目标为两部分数据所得到的参数$\theta_S$ 以及 $\theta_ T$
对比 多参数匹配、 单参数匹配、 Performance Matching三者之间差异:
1、单参数匹配和 Performance Matching之间差异:从公式上很好理解,单参数匹配中在计算 $\mathcal{L}$过程中同时还需要使用 源数据 和 蒸馏数据,由于只需要单步梯度,并且合成数据和网络的更新是解耦的,因此与基于元学习的性能匹配方法相比,这种方法更节省内存
2、单参数匹配和 多参数匹配之间差异:多参数匹配梯度分别通过源数据和蒸馏数据两部分进行更新得到,然后再去计算两部分参数梯度之间的差异更新蒸馏数据
- 3、分布式匹配
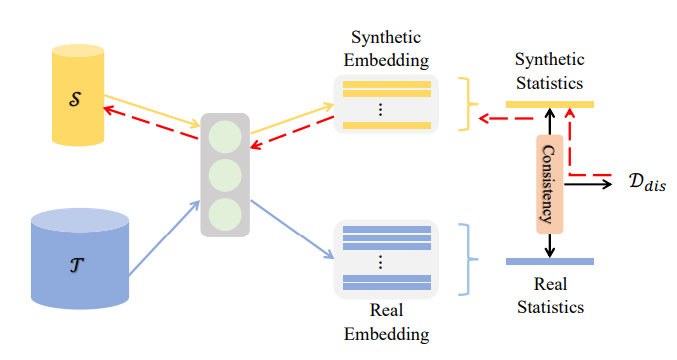
首先对于分布式匹配损失函数定义为:
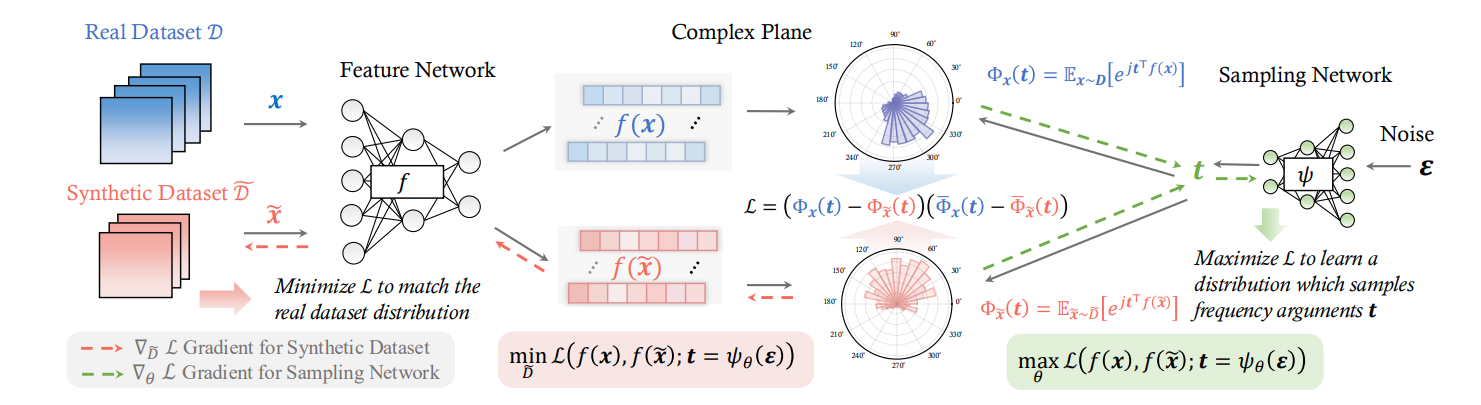
\[\mathcal{L}(S,T)=\mathbb{E}_{\theta \in \Theta}[\mathbb{D}(S,T;\theta)]\\ \mathcal{D}(S, T; \theta) = \sum_{c=0}^{C-1} \| \mu_{\theta,s,c} - \mu_{\theta,t,c} \|^2 \\ \mu_{\theta,s,c} = \frac{1}{M_c} \sum_{j=1}^{M_c} f_\theta^{(i)}(X_{s,c}^{(j)}), \quad \mu_{\theta,t,c} = \frac{1}{N_c} \sum_{j=1}^{N_c} f_\theta^{(i)}(X_{t,c}^{(j)})\](CVPR-25)上海交大论文
首先作者提到一点:通过分布式匹配进行数据蒸馏,容易导致无法获取分布的差异,进而导致效果不佳
参考
1、Dataset Distillation: A Comprehensive Review
2、A Comprehensive Survey of Dataset Distillation
3、(CVPR-2025)Dataset Distillation with Neural Characteristic Function: A Minmax Perspective
4、(CVPR-2024)On the Diversity and Realism of Distilled Dataset: An Efficient Perspective
5、(CVPR-2023)Accelerating Dataset Distillation via Model Augmentation